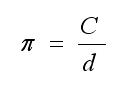With no disrespect intended to all those who believe in the existence of a supreme being, in this chapter we will attempt to “play God” and attempt the creation of a universe all of our own. We will assume from the very outset that we have an unlimited number of resources at our disposal. Our goal is to lay out some kind of master plan that will make it possible for a series of events to take place some time after everything has been set into motion. Although we will allow ourselves the possibility of “tinkering” with the evolution of our experiment and making some minor modifications here and there as the experiment proceeds forward, we will attempt to restrain ourselves and, instead of “fine tuning” the experiment without a moment’s rest as time goes on, we prefer to let things run on their own, taking instead the decision to exercise full control of whatever major events will happen in the future by a very careful selection of the initial conditions which take place when the experiment is set into motion. This assumes that there is a sentient intelligence at work (us) that has decided to make many interesting things happen. The alternate approach (random chance) is that even if we do absolutely nothing, indeed even if we do not exist, things will start to happen entirely on their own. But this latter approach assumes that something can be produced out of “nothing”, and by itself the notion of something coming entirely out of nothing is so repulsive to common sense that many people tend to disregard it even though it deserves some careful thought. As crazy as it may sound, the idea of a universe such as the one we live in having been created not just without any kind of prior planning but even being born entirely out of nothing is actually being given serious consideration by the academic communities around the world. [Many scientists and scholars with the highest academic credentials have mocked at the belief of others who are convinced that the universe came into existence due to the planning and work of a highly advanced intelligence, a "Supreme Being"; arguing that such belief is based solely upon faith which has no place in modern science. Yet, many of these same scientists are trying to convince the public at large to give serious consideration to the thought that everything came from absolutely "nothing", knowing well beforehand that it may never be possible to prove this statement, incapable as we are of duplicating in any laboratory here on Earth the very early initial conditions under which the Big Bang took place. Indeed, it seems very ironic to see faith being brushed aside from the panorama, just to be replaced by a formula-laden unproven belief that seems to require an even greater "leap of faith".] In his book Perfect Symmetry, Heinz Pagels expounds this point of view as follows:
“The universe began in a very hot state of utmost simplicity and symmetry and as it expands and cools down its perfect symmetry is broken, giving rise to the complexity we see today. Our universe today is the frozen, asymmetric remnant of its earliest hot state, much as complex crystals of water are frozen out of a uniform gas of water vapor. I describe the inflationary universe –a conjectured pre-big-bang epoch of the universe, which may explain some puzzling features of the contemporary universe, such as its uniformity and age, as well as provide an explanation for the origin of the galaxies. The penultimate chapter of this third part of the book –as far as speculation is concerned- describes some recent mathematical models for the very origin of the universe- how the fabric of space, time and matter can be created absolutely out of nothing. What could have more perfect symmetry than absolute nothingness? For the first time in history, scientists have constructed mathematical models that account for the very creation of the universe out of nothing.”
The models Heinz Pagels is referring to are models such as the one proposed by Alexander Vilenkin in 1982, who wrote a paper published in the journal Physics Letters entitled precisely Creation of Universes from Nothing. (Vilenkin resorts to a model in which the Universe is created by quantum tunneling from literally nothing into something known in general relativity as a “de Sitter space”, and after the tunneling the model evolves along the lines of the “inflationary” scenario). The hypothesis that the Universe we live in with all of its planets, all of its solar systems, all of its stars, all of its galaxies, all of its clusters of galaxies, all of its black holes, all of its quasars, all of its nebulae, and everything else contained inside, having sprung entirely out of nothing, has the undeniable appeal that it provides a very simple answer to a very difficult question. Indeed, it goes far beyond that: it provides the simplest possible explanation to one of the most difficult questions that can be posed by Man. Science itself has mostly been a quest to find simple answers to difficult questions, in the quest of its own Cabala. On the opposite side of the spectrum, we face the possibility that the answer to one of the most difficult questions of them all cannot be condensed in a few mathematical equations and that the “true” answer is so difficult for us to understand that such answer will perhaps be forever well beyond our powers of comprehension. Thus, we seem to face two choices: either a simple-minded answer, or no answer at all which we may be able to even attempt to grasp. And at this point in time there seems to be no middle ground that we can hold on to, at least not yet.
If we accept the hypothesis that the Universe we live in was born entirely out of nothing, and that the initial conditions without any guidance whatsoever somehow arranged themselves in such an extraordinarily lucky manner as to make it possible not just for the planets, stars and galaxies to appear but also for intelligent life to flourish, beating from the very beginning odds so insurmountable that the numbers defy imagination, then nothing more need be said regarding “nothingness” (please pardon the irony, it was unintentional), and we must be prepared to face the fact that pinging our hopes on “nothing” puts us directly on a head-on collision course and direct contradiction with many of the facts that have been presented on previous chapters. Nevertheless, the notion that an extraordinarily difficult problem can have such a simple-minded answer should be highly suspicious to some. Also, demanding that for something coming out entirely out of nothing with no prior planning whatsoever the initial conditions of the Big Bang will defeat the laws of probability and, despite random chance, everything will somehow arrange itself from the very beginning as to allow life to flourish some millions of years later after everything has “cooled down”, may push the limits of credibility of many people to such an extent that it may be easier to believe in the existence of the tooth fairy or Santa Claus than on the “random chance plus nothingness” approach. Besides, very few people in the academic community are attempting to tackle the even tougher issue of what could have preceded the primordial “nothingness” in the first place, and why there should have been a ”nothingness” to begin with [These insurmountable difficulties perhaps can only be overcome by assuming that such "nothingness" was actually preceded and produced by "something" which acted as a causative agent for the "nothingness". But then, the combined system, and by this we mean the "nothingness" together with the "something" taken both as a whole, is indeed "something" instead of "nothing". The only other alternative would be to assume that the "nothingness" was actually preceded by another "nothingness" which acted as a causative agent for the second "nothingness", in which case the combined system would still amount to "nothing". But then we are immediately confronted with an extremely difficult philosophical issue that will not go away: How can "nothing" be produced out of "nothing"? Most modern day philosophers will discard this latter alternative altogether on the grounds that even if nothing could be able to produce another nothing, the very act of popping "nothing out of nothing" is really quite "something" we would all like to see.]
Anyway, before proceeding, we must open ourselves to the possibility that indeed something may come entirely out of nothing. However, if we want some crucial events to take place long after the experiment has begun, and the initial conditions will be the determining factor in enabling those things to happen well into the future, then the “random chance” approach must necessarily assume that all the initial conditions, happening entirely at random, will somehow manage themselves from the very outset, without any planning whatsoever, to carry out an exquisite and wonderful act of creation and evolution instead of ending up as a big worthless mess. All the initial conditions must happen entirely at random but at the same time and by sheer accident they must also happen in the precise right manner. Becoming a true believer of this approach will require a major leap of faith (and in this respect, science would be no more different from some religion making the same demands). And remember: once the experiment is set into motion, we will not go back to correct mistakes, and it is very likely that any such mistakes will show up on a grand scale. Indeed, on a scale as grand as the Universe itself, it may be extremely difficult to hide mistakes. If the experiment fails, we may allow ourselves the possibility of just sitting back doing nothing with the hope that the experiment will repeat itself somehow (after all, if the Universe came from “nothing” without any kind of help whatsoever, why should we do anything at all to help stage an encore?), and watch the experiment taking place entirely on its own again, and again, and again, for what may very well be a long, long time; until we either get tired of waiting or we get extraordinarily lucky and something happens. But even with an eternity on our side, without any prior planning we may be stuck waiting forever with nothing good ever being accomplished. Hoping “random chance” alone, given enough time, will come to the rescue, will most likely be a very big disappointment for a would-be creator.
We will therefore proceed with the line of thought that the creation of a universe, far from being an act taking place entirely on its own without any kind of planning, left to its own good luck as it evolves, is instead an act which requires some foresight and some very careful planning before the creative explosion takes place. As we will soon see, even some minimal planning will require a science much more powerful than whatever we can muster at the start of the third millennium.
Before the act of creation is set into motion, we already know beforehand that to produce results it must allow for some strict rules to occur for which there will be no possibility of deviation. These rules, commonly known as “laws of nature”, are even today still being uncovered. These may be laws that are very similar to the same rules that a rider who wants to jump safely to the other side of a ditch must follow if he wants to survive the jump. Or they may be a different ball game altogether.
The first major stumbling block we would face in the setting of our initial conditions is that, according to the most recent theories, before the “Big Bang” which preceded the formation of the Universe time itself did not even exist, at least not as we know it today. And for that matter and to make things even worse, space itself did not exist either, at least not as we know it today. Indeed, the entire fabric under which the Universe is now evolving on a grand scale had no meaning at the very instant the Big Bang took place. This poses against us an extremely difficult problem which is well beyond our current level of understanding: as intelligent beings looking forward to carry out an act of creation which will take place even before the tapestry of the space-time continuum comes into being we are required as sentient beings to exist beyond the confines and limitations of space and time itself. This is something that we simply cannot accomplish, limited as we are to physical bodies that require in the most absolute terms the existence of a space-time continuum in order to function.
Just for the sake of argument, let us assume that somehow we are able to function effectively beyond space-time itself (and even then it becomes extremely hard to imagine how we would be able to reason, since any chain of reasoning requires a flow of time in order to begin with some basics and arrive at certain conclusions); and in order to make this possible we will postulate the existence of something we will call “Super-Time”, a higher level of dimensional reality inside which time itself can be created and destroyed at will. Lacking words to even try to describe such alternate reality, we will simply assume what may be and push on forward with our grand project. If we are to be true creators, our next goal could be to enable our creation to become aware of its own existence. And how can we enable our creation to become aware of its own existence? By allowing intelligent life to appear and flourish in the Universe we have created! This goal might very well be the greatest challenge in our creation, since it demands no less from us than to come up with a reasonable solution to the problem of designing living beings capable of evolving all the way up to order ζ (and possibly even beyond that). And as we have already seen, the goal of allowing life forms to come into being and flourish demands almost immediately the selection of other initial conditions without which life will simply not emerge.
As a next step in creating our own universe, we might try to change some of the physical laws that govern the workings of this universe. Take, for example, Newton’s law of universal gravitation, stated as follows:
“Two bodies attract each other with a force that is in direct proportion to the product of their masses, and that varies inversely as the square of the distance that separates them.”
Stated in mathematical terms, if we identify the masses of the two separate bodies as m1 and m2, and call the distance between the centers of the two bodies r, then Newton’s law can be stated simply as follows:
The constant G is the well-known constant of universal gravitation, a constant that has to be determined experimentally.
Since we are writing our own rules, we could try to design our own law of universal gravitation. It could go as follows:
“Two bodies attract each other with a force that is in direct proportion to the product of their masses, and that varies inversely as the cube of the distance that separates them.”
Notice that gravitational attraction will now depend upon the inverse of the cube of the distance that separates the two masses instead of the inverse of the square of such distance. In mathematical terms, our own universal law of gravitational attraction would be:
This new law would still produce a similar (though not equal) effect as the previous one. As the two bodies are brought closer and closer to each other the gravitational attraction between them grows exponentially, and as they are separated further and further from each other the gravitational attraction drops sharply. And when the bodies are very far apart, the gravitational attraction between them can be considered negligible.
Up to now, all is well, except for one bothersome detail. It can be shown through other mathematical tools (specifically, a theorem known as Gauss’s theorem) that the number two exponent in the denominator of the original law, r², is a direct consequence of the fact that the surface area of an imaginary sphere surrounding any given body is given by the formula A = 4πr². Thus, the number two exponent is not as arbitrary as it might have looked at the beginning. And this is not physics; it’s mathematics. In order to change the exponent from the number two to the number three, we must be ready to overhaul geometry itself. Unless the exponent is exactly the number two, and by this we mean that a number such as
2.00000000000000000000000000000000000000000000000000000000001
would be an unacceptable replacement, then geometry must be overturned. Even if we could do this, it must be taken for granted that the replacement would complicate enormously the design of our universe. As a way out, we might wish to recall that this Newton’s law of universal attraction was made obsolete with the coming of Einstein’s theory of relativity. However, this is no consolation either, for the theory or relativity itself is firmly based in geometry [actually, the theory of relativity allows for three different types of geometries, one of them being the well-known Euclidean geometry, and the other two belonging to the category of non-Euclidean geometries: Bernhard Riemman's elliptic geometry, and the Bolyai-Lobachevski hyperbolic geometry. However, each one of these geometries have their own rigid set of axioms from which some mathematical relationships invariably must follow. The results are always derived from the set of axioms, and not the other way around], so much so that it is often called geometrodynamics. Even if somehow we can get away with changing the value of the integer number 2 that appears as exponent in all of the “inverse square” type of laws, this could have immediate repercussions in how the universe we are designing would work, and to cite just one among the many possible consequences we could mention the fact that the basic particles that make up all visible light and electromagnetic radiation (the photons), which have no mass, would immediately acquire a mass solely on this account. We can read at the beginning of the book Classical Electrodynamics by John D. Jackson the following:
“The distance dependence of the electrostatic law of force was shown quantitatively by Cavendish and Coulomb to be an inverse square law. Through Gauss’s law and the divergence theorem this leads to the first of Maxwell’s equations. The original experiments had an accuracy of only a few percent and, furthermore, were at a laboratory length scale. Experiments at higher precision and involving different regimes of size have been performed …the test of the inverse square law is sometimes phrased in terms of an upper limit on mg (the mass of the photon) … the surface measurements of the earth’s magnetic field give slightly the best value, namely that mg is less than 4 •10-48 grams … For comparison, the mass of the electron is me = 9.8 •10-28 grams … We conclude that the photon mass can be taken to be zero (the inverse square law holds) over the whole classical range of distances and deep into the quantum domain as well. The inverse square law is known to hold over at least 24 orders of magnitude in the length scale!”
As the reader can glean from the above quotation, just a small change in the integer 2 exponent of the inverse square law would not only assign a mass to the photon; it would also require a major modification of the basic laws of electromagnetism, and the replacement will surely do away with Maxwell’s “simple” basic equations requiring them to be replaced by something which, at least from the perspective of mathematics, will definitely be much uglier. And all these changes in the way electromagnetism works may have such a profound effect in the way our creation develops that not only it may not be habitable, it may turn out to be impossible to create a long lasting stable universe under such conditions. But as we have mentioned already, even before we may attempt to implement such a change we must figure out what we would use to overhaul geometry and replace it with something else, a task illogical enough to send any would-be-creator to an asylum. Thus, our hands appear to be tied down, and we seem to have no choice of selection here.
Not to be discouraged, we might try changing the values of some other physical constants that are not a direct consequence of some universal logical requirement from the science of mathematics, physical constants whose values cannot be fixed nor predicted by mathematics alone, physical constants that are measured in a laboratory. One physical constant that comes to mind is the speed of light, represented by the letter c. The speed of light, the basic building brick of the special theory of relativity with a known value of about
c = 299,793,000 meters per second
could be set by us to a smaller value. This seems like an awfully big speed, and we might be tempted to use a much smaller value in designing our own universe. Perhaps we could set up our initial conditions in such a way that the speed of light would come up to be something like one thousand meters per second:
c = 1,000 meters per second
But as trivial as the change might appear to be, this change would most certainly have dramatic effects on the evolution of our universe. If the special theory of relativity is to remain valid –and for the time being we will assume it will-, then using such a small value for the speed of light would make life extremely hard for whatever intelligent life forms we would expect to see evolve in our universe –if anything can evolve at all-. Strange phenomena would show up everywhere, such as time dilation, length contraction, a total obvious loss of the concept of simultaneity, objects increasing in mass while accelerating, and so forth. Phenomena such as length contraction would not be merely an optical illusion, it would be something confirmed by actual measurements using precision instrumentation. The same thing would happen in the case of time dilation. Clocks would be almost impossible to synchronize, since under special relativity there is no such thing as a universal time, there are only local times (the formal term used is proper time). All of these strange happenings are fully predicted by the special theory of relativity, and life forms evolving in such an outlandish universe would sooner or later have to grow accustomed to such effects. George Gamow (well known for predicting the cosmic microwave background radiation shortly before it was discovered by Penzias and Wilson, and for his theory of “quantum tunneling” that successfully explains the enormous variation observed in the mean lifetime of radioactive materials) wrote a series of stories contained in the book Mr. Tompkins in Paper Back where, in one of the stories, Mr. Tompkins visits a dream world in which the speed of light is 10 miles per hour and relativistic effects become quite noticeable. We can read the following in Gamow’s book:
“A single cyclist was coming slowly down the street and, as he approached, Mr Tompkins’ eyes opened wide with astonishment. For the bicycle and the young man on it were unbelievably shortened in the direction of motion, as if seen through a cylindrical lens. The clock on the tower struck five, and the cyclist, evidently in a hurry, stepped harder on the pedals. Mr Tompkins did not notice that he gained much in speed, but, as the result of his effort, he shortened still more and went down the street looking exactly like a picture cut out of cardboard … Mr Tompkins realized how unfortunate it was that the old professor was not at hand to explain all these strange events to him … So Mr Tompkins was forced to explore this strange world by himself. He put his watch right by the post office clock, and to make sure that it went all right waited for ten minutes. His watch did not lose. Continuing his journey down the street he finally saw the railway station and decided to check his watch again. To his surprise it was again quite a bit slow.”
If the special theory of relativity is fully valid in our own Universe, then we must take for granted that these effects are also a daily occurrence in our Universe, so why don’t we ever see such bizarre things taking place in our everyday lives? Precisely because the speed of light is so large. In order to witness such effects, we should be moving at speeds very near the speed of light, and at present we do not have yet the technology to travel at such speeds. However, in many experiments carried out around the globe where the speed of light is almost matched, e.g. in particle accelerators used to study subatomic particles, these effects do indeed occur, and physicists constantly witness and measure phenomena that fully confirm the predictions of the special theory of relativity. When we move at relatively “slow” speeds such as the speed of sound, relativistic effects are not noticeable and we perceive the illusion that there really is an absolute time, that there are no such things as length contraction and time dilation. But this is just an illusion. The effects are there, too small to be noticed by our ordinary senses, but they are there. Besides the rather outlandish effects that would have to be confronted by any species living in a universe where the speed of light is small, there would also be some other very undesirable consequences, and perhaps the major consequence would derive from the fact that information cannot be conveyed any faster than the speed of light. Under this scenario, in order to use a cellular phone one party would have to talk to the other party fully aware that his voice could be arriving with a delay of several minutes depending on how far the other party is located away from him, which means that after he has finished talking he would have to wait at least the same amount of time in order for his message to arrive complete, and thereafter he would have to allow an additional time frame to give the other party a chance to send a reply, a time frame that would have to include the time required by the other party to convey his/her message plus the time it would take for that message to travel to him at their rather “limited” speed of light. [Something like this actually takes place when we try to relay orders to a space probe like Voyager or Galileo out in deep space, because the orders we send out to such space probes or the information we get from them may take several minutes to arrive from one end to the other. For example, when the Earth and Mars are close to each other, sending out a message to Mars takes a little more than four minutes to reach its destination, whereas a message from the Earth to Jupiter may take close to half-an-hour.] Radio communications would thus be a real nightmare. The Internet, fully dependent upon microwave links and satellite communications that use radio signals traveling at the speed of light, would not exist. Many technological advances we now enjoy and take for granted would be rendered completely useless in such a universe, and life under such conditions may not just be intolerable, perhaps it would be impossible. For any being living inside such alternate universe, it would not just bear the mark of a bad design; it would bear the mark of a very bad design.
Not to be outdone, as an alternative to our design we might try to raise the speed of light to a higher value instead of lowering it. This would have the advantage for those beings living inside our alternate universe that communications using any type of radio signals would be much faster, and since no information can be conveyed at a speed faster than the speed of light raising this limit would certainly appear to open up a new world of possibilities. So, let us increase the value of the speed of light tenfold to its new value
c = 2,997,930,000 meters per second
At this point all appears to be well, until we recall one of the most famous formulas derived by Albert Einstein from the special theory of relativity:
E = mc²
This formula essentially tells us that energy and mass are completely equivalent, and both can be taken to be two different manifestations of the same thing. In our alternate universe, all we have done was to increase the speed of light tenfold, assuming that everything else remained the same, including the mass of individual atoms. But notice that by increasing the speed of light tenfold, we have actually increased the equivalent energy content of any atom one hundredfold (because of the squared exponent for the speed of light in the above formula). On a small scale, one immediate consequence this would have would be to make many of the “stable” elements and compounds in nature very unstable. Indeed, they would become radioactive. With a lot of radioactivity to go around, it is hard to imagine how any life form could subsist under such harsh conditions, and how it would be able to preserve itself and its genetic code from damage for a long enough period of time (the only possible exception that comes to mind is the radiation-resistant bacterium Micrococcus radiophilus, which can withstand enormous doses of radiation, but even it can be killed in massive quantities with a strong enough source of radiation). Evolution would not be able to produce its wonders in such an alternate universe, for even if it is able to work itself around overwhelming odds, in order to juggle with such odds it requires a relatively stable (non-radioactive) environment for a long period of time (we have not yet seen any new life forms capable of adapting and surviving in the environment of Chernobyl, and most likely we never will). On a large scale, such an increase in the energy content of atoms and molecules would increase gravitational effects enormously, and many of the stars and galaxies whose existence today we take for granted would not be able to survive long under our dictum. They would quickly compress themselves and collapse into black holes and neutron stars, and the universe would be a very spooky dark place with no stars shining anywhere in the sky. With such instability at very small scales and very large scales, it is not hard to foresee that our alternate universe will be short-lived. Fortunately, there would be nobody around to witness the mess.
In order to create our own universe with our own rules, with initial conditions of our own choosing, the theory of relativity seems to be standing in the way, so much so that Steven Weinberg has often been quoted as saying:
“Quantum mechanics without relativity would allow us to conceive of a great many possible physical systems … However, when you put quantum mechanics together with relativity, you find that it is nearly impossible to conceive of any physical system at all. Nature somehow manages to be both relativistic and quantum-mechanical; but these two requirements restrict it so much that it has only a limited choice of how to be.”
So, perhaps we should be thinking of doing away with relativity altogether, using something else instead. But what? Einstein’s theory of relativity, as counterintuitive and complex as it may appear to many, is simplicity itself in comparison to many other physical theories and models of the universe. Other alternate theories to Einstein’s relativity such as the Dicke-Brans-Jordan theory of gravity (1959-1961) and the Wi Ni theory of gravity (1970-1972) have been proposed that would apply to this universe, but when put to the test in their power of prediction and confirmation of experimental data, the only one that has survived is Einstein’s theory of relativity, undoubtedly because it is a purely geometric theory describing a four-dimensional space-time continuum. Still other possible alternatives to relativity such as the “spin-two field theory of gravity” have been found to be internally inconsistent, ending up in the graveyard before they could even be tried out. In order to do away with relativity, we must be prepared to come up with something else that will not be as simple as relativity, something that will surely be much more complex. But then we will not allow our alternate universe to be able to develop from simple fundamental principles. If the task of creating (and by this we mean selecting the proper initial conditions) a universe such as the one we already live in seems hard enough, the task of creating an alternate universe where relativity is not required appears to be intractable. For the time being, we must be prepared to accept relativity as a fact of life in almost any conceivable logical universe we may attempt to design.
If a priority in the design of our universe is to allow intelligent life to flourish and even wonder about its origins, we might be forced to use a speed for light that will neither be too large nor too small, not necessarily the same as the one we are used to, but perhaps just a little bit different from the value we already know that works. True, we will not be displaying much creativity and originality, but there is no big merit in starting from scratch if we know that all we may end up with is a big mess. So, let us settle for a slightly different value for c, say:
c = 300,500,000 meters per second
This value perhaps may still allow for the creation of a viable universe with intelligent life inside. After all, what could possibly go wrong with such a minor departure from the value we are all used to?
There are other physical constants we might attempt to fiddle with. For example, Planck’s constant h, the very foundation of what we know today as quantum physics, with a known value of about
0.000,000,000,000,000,000,000,000,000,000,006,625,17 joule • second
could perhaps be set to a slightly lower value without any major consequence, such as
0.000,000,000,000,000,000,000,000,000,000,006,600,00 joule • second
There are still more physical constants we might try to tinker with, such as the electric charge of an electron or the mass of the proton. What harm could possibly come from using slightly different values from the ones we already know have worked in the successful creation of a universe that harbors intelligent life? We would hope that, in the long run, things would settle themselves somehow on their own and a slightly different but viable universe would still emerge.
Would it?
The stark reality is that we just don’t know.
It is possible that such small changes would not make a big difference in the grand scheme of things. But it is highly probable that they would. Einstein’s equation for general relativity that is the cornerstone of all modern cosmological theories:
G = 8πT
where the left-hand side of the equation describes the curvature introduced into the space-time continuum by the presence of mass-energy on the right-hand side of the equation, is essentially a set of nonlinear differential equations (G and T are mathematical objects we call tensors and thus the equation is a tensor equation). And, as we saw on Chapter Five, it was precisely the differing simulation results obtained due to the nonlinear nature of the model used by Edward Lorenz that led him to the conclusion that long-range forecasting was impossible (to be honest, the models used by Edward Lorenz also possessed the characteristic of recursiveness, which require for their numerical evaluation that once a small result has been obtained for the set of equations this result be fed back again as an initial condition into the same set of equations in the hopes of converging into a more accurate answer which will in turn be used again as an initial condition, with this process being repeated for a usually long number of cycles; and since the equations for general relativity cannot be solved exactly under many conditions due to their nonlinearity, it is very likely that a numerical computer simulation used to obtain an approximate result would have to resort to some type of recursiveness in order to converge into a desired solution for the equation, predicting a different outcome). For the time being, let’s set aside the thorny issue of the impact that non-linearity will have upon the evolution of our alternative universe when small changes are introduced from the very beginning on the current values of known physical constants.
One thing is certain. If at this very moment some change was to be introduced in the entire universe, it could have measurable consequences. A famous question once posed by Henri Poincaré goes as follows: If last night while everyone slept everything doubled in size, would there be any way of telling such a thing had occurred? Poincaré replied no. If everything, including all the yardsticks, all the rulers, all the tape measures, everything would have doubled in size, then we would have no way of knowing that the change had taken place. Such was the common wisdom at the time. However, as William Poundstone explains in his book Labyrinths of Reason:
“In 1962 and 1964 papers, (Brian) Ellis and (George) Schlesinger claimed that the doubling would have a large number of physically measurable effects. Their conclusions depend on how you interpret the thought experiment, but they are worth considering … For instance, Schlesinger claimed that gravity would be only one-fourth as strong because the earth’s radius would have doubled while its mass remained the same. Newtonian theory says that gravitational force is proportional to the square of the distance between objects (in this case the center of the earth and falling objects at its surface). Doubling the radius without increasing the mass causes a fourfold reduction in gravity … Some of the more direct ways of measuring this change in gravitational pull would fail. It wouldn’t do to measure the weights of objects in a balance. The balance can only compare the lessened gravitational pull on objects against the equally lessened pull on standard pound or kilogram weights. Schlesinger argued, however, that the weakened gravity could be measured by the height of the mercury column in old-fashioned barometers. The height of the mercury depends on three factors: the air pressure, the density of mercury, and the strength of gravity. Under normal circumstances, only air pressure changes very much … The air pressure would be eight times less after the doubling, for all volumes would be increased 23 times, or eightfold. (You wouldn’t get the bends, though, because your blood pressure would also be eight times less.) The density of mercury would also be eight times less; these two effects would cancel out, leaving the weakened gravity as the measurable change. Since gravity is four times weaker, the mercury would rise four times higher –which will be measured as two times higher with the doubled yardsticks. That, then, is a measurable difference … There is also the question of whether the usual conservation laws apply during the expansion. Schlesinger supposes that the angular momentum of the earth must remain constant (as it normally would in any possible interaction), even during the doubling. If the earth’s angular momentum is to remain constant, then the rotation of the earth must slow … There would be other consequences of conservation laws. The universe is mostly hydrogen, which is an electron orbiting a proton. There is electrical attraction between the two particles. To double the size of all atoms is to move all the electrons ‘uphill’, twice as far away from the protons. This would require a stupendous output of energy. If the law of conservation of mass-energy holds during the doubling, this energy has to come from somewhere. Most plausibly, it would come from a universal lowering of the temperature. Everything would get colder, which would be another consequence of the doubling. There are thousands of changes; it is as if all the laws of physics went haywire. The doubling theory would quickly be confirmed and established as scientific fact.”
The fact that in this dilemma posed by Poincaré common wisdom went unchallenged for so long and only until recently this question was addressed in a credible manner taking as a basis our known natural laws is a clear indication that there is still a lot of work to be done in this field. Indeed, by applying the knowledge we already have it should be feasible to study the possibility of alternate universes and whether such universes with different values for important physical quantities such as the charge of the electron would be similar or perhaps would have to be vastly different from our own. A lot of work has been done in this area recently, still much more work needs to be done.
Even if we set aside completely the impact that nonlinearity might have on the long run upon the evolution of alternate universes whose physical constants are slightly different from those in our own Universe, we must now recall –in case we may have forgotten- from Chapter Nine the observations that were made indicating that the successful evolution of our Universe was critically dependant on many physical constants (such as the fine structure constant) and other “design” parameters lying inside a very restricted range of values. Any individual alterations beyond a rather narrow margin, beyond even one percent of their current value, would have been more than enough to make the alternate universe fail to satisfy the anthropic principle, resulting perhaps in such minute quantities of carbon being made that there would not have been on planet Earth enough material to build even a dozen flies. This does not mean that it may be impossible to build another universe by changing the values of universal physical constants. What it does mean is that if another universe is to be viable at all, we may have to modify in some manner all of the physical constants and not just one or two; and if all of the constants are being modified it would have to be done with the utmost care by keeping a very delicate balancing act in order to meet simultaneously many requirements demanded by the anthropic principle. In other words, if we attempt to modify the speed of light just a little bit, we may be forced to start modifying the rest of the physical constants one by one until at the very end we will have found it necessary to modify all of them, with each change requiring a very careful design selection in order to make ends meet. Thus, what the future inhabitants of the universe would take as just a large conglomerate of extraordinarily lucky coincidences would really be the result of a deliberate selection between many (perhaps conflicting) design options.
Before we attempt to change important physical constants such as the speed of light or Planck’s constant, there is still a more important issue that needs to be addressed: Are these constants truly fundamental universal constants, starting points which at least in theory could be varied and their consequences could still be explored? Or are they derivable constants, not fundamental quantities but quantities that can be derived from something perhaps more fundamental? Because in the latter case, we would simply have no choice in the creation of an alternate universe. This question is so profound in its ramifications and philosophical consequences that Albert Einstein who was a firm believer in a supreme being who preceded the act of creation is often quoted as saying: “What really interests me is whether God had any choice in the creation of the world”, adding:
“Concerning such (dimensionless constants) I would like to state a theorem which at present cannot be based upon anything more than upon a faith in the simplicity, i.e., intelligibility of nature: there are no arbitrary constants of this kind; that is to say, nature is so constituted that it is possible logically to lay down such strongly determined laws that within these laws only rationally completely determined constants occur.”
Under this scheme, the constants that provide physics its starting point would be completely determined. Their numerical values cannot be changed, not without destroying the theory itself. But even here there could be some freedom of choice, for in his conjecture Einstein talks about laying down strongly determined physical laws, and in laying down those laws from which everything else will be derived we are in fact designing a universe.
The suspicion that some of the physical constants we are now measuring could be more universal than we might think is not without merits. We may recall from the first chapter of this book that in the problem of the rider who was trying to clear the ditch, the problem was essentially a problem in geometry and the only time physics entered into the scene was with the “universal” constant g of 32 feet per second per second, the downward acceleration pull due to gravity. But this “universal” constant g is no “fundamental” constant at all! It can, in fact, be derived from the more universal constant of gravitation G. And this value of g is only valid approximately near the surface of the Earth, and minute differences in the value of g are routinely used every day by geologists and prospectors in order to find mineral and petroleum deposits. [The famous Italian physicist Galileo Galilei of the late sixteenth and early seventeenth centuries became convinced, after measuring the value of g with the help of spherical objects rolling along over inclined planes, that the value of g was a universal constant, so much so that in the famous experiment where he is supposed to have dropped objects of different weights from the leaning tower of Pisa, he was able to predict that they should take exactly the same time to reach the ground. On the surface of Mars the value of g is close to 12.9 feet per second per second, so a person weighing 200 pounds on Earth would actually weigh some 80 pounds on Mars; and on the surface of the Moon where g has a value of 5.47 feet per second per second, about one-sixth the value of that on Earth, the same person would weigh only about 34 pounds; and thus anybody from Earth could actually jump on the Moon like Superman where it not for the bulky space suits required to survive there.] Both the problem of the rider trying to clear the ditch and Einstein’s theory of relativity are essentially of a geometrical nature, with the “fundamental physical constants” intervening only to fix the shape of the geometry that will apply to the problem in question. On the other hand, the values of other “fundamental” constants in nature can be fully determined with any level of precision we desire not by taking any actual measurements but just by counting numbers. Take, for example, the well-known mathematical constant π (pi), known to have a value close to
π = 3.141,592,653,589,793,238,462,643 …
This constant appears rather frequently in the formulation of many problems in geometry. For example, if we are given a circle with a known radius we might call r, then it can be shown that the area enclosed inside the circle is given by the formula:
A = πr²
Another formula where the constant p crops up is when we are trying to determine the length C of the circumference that surrounds a circle of diameter d:
C = πd
In the latter formula, once the diameter d is fixed then the circumference C will automatically also become fixed. We have absolutely no choice in selecting any length C we might desire for our circumference that is not compatible with the given value of the diameter d, since their relationship is preordained by geometry. The only way we could have a circumference whose length is not related to the diameter of the circle it encloses by the above formula would be to overhaul geometry and replace it with “something else”, a thought that would certainly horrify many mathematicians.
With so much depending upon the value of the constant π, it appears we would like to be able to determine the value of this constant with the best precision we can come up with. To a young student making his way through high school, it would seem that the obvious choice to determine the value of the constant π would be to actually measure it. Indeed, if we take the latter formula, we can rewrite it as follows:
From this vantage point, the definition of π as a universal constant would be something like “It is the number that results when we divide the circumference C of any given circle by the diameter d of the circle it encloses”. The young student would perhaps then draw a circle of about two inches in diameter, and by using a flexible tape he would measure the circumference of the circle to be about 6.4 inches. Applying the formula he would obtain a preliminary value for π of about 3.2; after which he would take more careful measurements finding out that the diameter of his circle was in fact close to 2.1 inches while the circumference would have a value of about 6.60 inches, whereupon application of the formula would yield a closer value for π of about 3.14. Notice that the size of the circle is irrelevant; if he had used a circle with a diameter twice as large then the circumference would have also doubled in length so as to make the constant π still able to come up with the same value. Geometry remains in full control regardless of the size of the object we are studying. As his measurements improved, he would get an ever more accurate value for π. However, the method of determining the value of π by measurements alone has a major limitation: the accuracy can only go so far as our ability to measure precisely. With the added knowledge that the sequence of decimal digits in π is known to be infinitely long, the measurement technique will most likely fail to live up to any major expectations.
There is another method of knowing the value of π that is not based on taking any kind of measurement. It is based on sheer mathematics alone. It is based on counting numbers. It can be formally proven that the value of π can be computed to any desired level of accuracy by using formulas such as the following one:
If a person tries to obtain the value of a constant like π by measurement alone (experimentally), then that person is thinking like a physicist. If a person tries to obtain the same value by counting numbers (theoretically), then that person is thinking like a mathematician.
In the book Theories of Everything, John D. Barrow makes the following observations:
“As science has progressed and become more searching in the questions that it addresses to the world of reality, it is no longer content to regard those constants of Nature as standards that we can now by measurement alone. Even those negativists who at the turn of the century thought the work of physics was done save for the increasingly accurate measurement of the constants of Nature did not envisage that there might exist the possibility of calculating their values. They did not have such a programme on their agenda. The modern seekers after the Theory of Everything believe that ultimately some deep principle of logical consistency will permit these constants of Nature to be determined by simple counting processes … A theory that could successfully predict or explain the value of any constant of Nature would attract the attention of every living physicist.”
Surely, if a truly universal constant in Nature such as π can be evaluated not by taking any measurements but just by counting numbers, shouldn’t we expect the same from all of the other “universal” constants, including physical constants?
Professor Heinz Pagels makes the following observation in his book Perfect Symmetry:
“At higher energies, physicists have calculated the other distance scales we have discussed, so that we have a hierarchy of distances … Between these microscopic distances nothing much happens –unlike the situation for much longer distances- … By taking ratios of the above three distance scales (so the fact that we chose centimeters to measure the distance drops out), we obtain the large pure numbers 1013 and 1017. These numbers demand an explanation. What are they doing in nature? From the standpoint of (Grand Unified Theories) or any other theory, these numbers, representing the hierarchy of distance scales in nature, are today without explanation. These are ‘arbitrary constants.’ Physicists want to explain these numbers and solve the ‘hierarchy problem.’ But so far, although there are some intriguing hints, a solution has eluded them. Even (Grand Unified Theories) have ‘arbitrary constants’ and cannot be the final unified-field theories.”
Attempts to derive physical constants from “something else” range from efforts such as the one displayed by Sir Arthur S. Eddington –considered by some to be the greatest astrophysicist of the pre-World War II era- in his books The Philosophy of Physical Science and Fundamental Theory (the latter assembled and published posthumously from his notes) where he attempts to derive all of nature’s physical constants such as the mass of the electron and Planck’s constant by juggling numbers and taking as a starting point certain a priori epistemological considerations; to the less mystic and more heroic efforts of the unified field theories and string theories coupled with attempts to describe the Universe with a cosmic wave function (a preliminary step in this direction was pioneered by Stephen W. Hawking and James B. Hartle in 1983 when they were able to come up with a model that can describe the quantum state of a spatially closed universe by means of a cosmic wave function analogous to the wave function used to describe atoms and elementary particles, a cosmic wave function that determines the initial conditions of the universe and according to which the distinction between the past and the future disappears in the very early universe with the “time” direction taking the properties of the “space” direction by having no actual “beginning” just as there is no edge to three-dimensional space). The problem with any theory of this type is that in order for it to be a correct description of Nature it has to assume that we already know what the fundamental constituents of Nature are. And to date we are still unsure as to what the fundamental constituents of Nature are. Near the turn of the century it was thought that the major constituents of all matter were the atoms. But then it was discovered that atoms are made up of even more fundamental constituents: the proton, the electron and the neutron. Eventually, more fundamental constituents were found as more and more subatomic particles were discovered (such as neutrinos, mesons, pions, etc.) all the way down to leptons and quarks that were later presented to us as “being truly fundamental”. But “fundamental” particles remain so as long as nobody has any access to even more powerful particle accelerators. It is conceivable that with much more powerful particle accelerators such as the Superconducting Super Collider (killed by the U.S. Congress before it could ever go into operation) we could discover that there are even more “fundamental” particles, perhaps “rishons” and “antirishons”; with the discovery process repeated over and over, perhaps going further back endlessly and hopelessly into more and more “fundamental constituents” [one cannot help but recall the following 1733 verse from Jonathan Swift: "So, Nat'ralists observe, a Flea Hath smaller Fleas that on him prey, And these have smaller Fleas to bit 'em; and so proceed ad infinitum"]. During the latter part of his life, after fully developing his theory of relativity, Einstein himself set out to develop a “grand unified field theory” (no doubt inspired by the short-lived success of the unification of relativity and electromagnetism accomplished in 1921 by mathematician Theodor Kaluza who assumed a geometrical five-dimensional space) that would include “everything” and would explain “everything”, but he realized that his efforts would at best be incomplete when confronted with the experimental data confirming the existence of other particles and forces he could not have anticipated theoretically. Thus, before we attempt to derive the constants of Nature from something more fundamental, we need to be absolutely certain that indeed what we call fundamental is fundamental. For the time being, the best we have gives nary a hint on the real fundamental nature of all the initial conditions required for the creation of this Universe (beginning with its basic constituents), let alone the possible constituents we might try to use to design and build an alternate universe.
Before going any further, let us consider the problems we might run into while trying to design an alternate universe by defining the values of those physical constants we choose to consider “fundamental”. For simplicity, we will assume that such universe is made up of things like the ones we have already found in this universe, e.g. atoms made up of protons and electrons, light, etc. For the sake of argument, let us assume that we arbitrarily devise formulas that will enable us to derive all of the known important physical constants from just two single fundamental quantities that cannot be derived from anything else. [To be honest, the modern approach in trying to derive most everything from things more fundamental in Nature such as a single "unified force" -that tries to explain all interactions between subatomic particles- is based upon symmetry considerations, and it is the breakdown of symmetry of a single force from where everything else is supposed to start. This breakdown of symmetry takes place in a number of mathematical models of quantum field theory such as the Glashow-Salam-Weinberg model of leptons. However, besides requiring a Ph.D. degree in Physics for its understanding, a detailed discussion of this topic would lead us far astray from our original objective, and would not alter much the essential points being discussed here.] And let’s give these quantities a name; say α (the Greek letter alpha) and β (the Greek letter beta). The speed of light c, Planck’s constant h, the mass me of the electron, and the electric charge qe of the electron perhaps could be derived from these quantities from hypothetical formulas such as the following:
c = 5α + β
h = 2αβ
me = 10αβ
qe = 9αβ
h = 2αβ
me = 10αβ
qe = 9αβ
Suppose that in our grand design we want the speed of light c to have a value of ten units (for the time being we will relax the requirement of allowing life to evolve in our design). There are many possible combinations of values we can choose for α and β. We could give α the value of 1 unit and β the value of 5 units. This way, the speed of light in our creation comes out to be 10 units, just as we ordered it to be. But the selection of these two values will have an immediate “cascade” effect on all of the other physical constants. Planck’s constant h will immediately acquire a value of 10 units, the mass of the electron me will have a value of 50 units, and the charge of the electron qe will have a value of 45 units. Whether this choice of values can lead to anything worthwhile is an entirely different matter. We might notice that the values for the speed of light c and Planck’s constant h are of comparable magnitudes. Ordinarily, we would like the speed of light c to be as large as we can possibly make it in comparison to Planck’s constant h. In order to achieve such purpose, we could use small values for α and β, the smaller the better since in the formula for c they add up but in the formula for h they multiply themselves. Thus, if we set α to be 0.01 units and β to be also 0.01 units, the speed of light turns out to be 0.06 units whereas Planck’s constant h turns out to be 0.00004 units. And this has the added desirable effect that both the mass and the charge of the electron also become much smaller. But we have no choice in the specific values we may want the latter to take. We must be ready to accept whatever values we get according to our formulas.
Since we have two independent “fundamental” constants a and b from which we are trying to derive four physical constants (c, h, me and qe), we suspect that we should be able to choose and predetermine any pair of values for two of those four physical constants, with the values of the remaining two other physical constants being preordained by the formulas. Thus, if we want the speed of light c to have a value of twelve units and at the same time we also want Planck’s constant h to have a value of eight units, then we can determine with simple algebra that this can be achieved if our “fundamental” constants are given at the moment of creation the following values:
α = 2 and β = 2
As a matter of fact, this is the only combination of values for α and β in our design that will give the speed of light c a value of twelve units and Planck’s constant h a value of eight units. The two remaining physical constants will automatically acquire the values of forty units (for the mass of the electron me) and thirty-six units (for the charge of the electron qe) according to the formulas we have devised. Thus, it appears that we have free will in giving any two of our derived physical constants any value we so desire. But this is not so. For example, if we want to give the speed of light c a value of one unit and Planck’s constant h a value of ten units, then it is not hard to prove using elementary algebra that there is no possible combination of values for α and β that will give under the above formulas a speed of light c with a value of one unit and a value of ten units for Planck’s constant h. Thus, again it appears that our hands appear to be tied down, at least partially.
The fact that under the above scheme of formulas we can only assign freely the values of two “derived” physical constants if we start out with just two “fundamental” constants goes much deeper than the formulas themselves, for even if we try to modify the formulas, the basic limitation will remain. It doesn’t matter what type of formulas we may try to come up with; as long as we have more “derived” physical constants than “fundamental” constants there will always be some “derived” physical constants whose values will be automatically preset by the formulas, beyond our control. In more formal jargon, the limitation comes from the fact that in our formulas the number of independent variables exceeds the number of dependent variables. The only way in which we can have full control over the values we can assign to all of our “derivable” physical constants would be to have as many “fundamental” physical constants as we have “derivable” constants. Thus, in the above example we would need two more “fundamental” physical constants, call them γ (the Greek letter gamma) and δ (the Greek letter delta). Then we can come up with many choices of formulas to assign whatever value we want to our four “derivable” physical constants independently from each other. We would have full control of our design down to the last detail. But at this point we should realize that we are really kidding ourselves, for if we have as many “fundamental” constants as we have “derivable” physical constants, we might just as well do away with the concept of “fundamental” constants altogether and consider our “derivable” physical constants as the fundamental physical constants in the universe we are trying to design, capable of receiving independently from us any arbitrary value we might want to give them. No arbitrary formulas or relationships for deriving our fundamental physical constants from something else would be required. Another immediate consequence of following this approach is that in the design of our universe we would have each and every one of our fundamental physical constants forming a set of initial conditions that we can vary at will to any set of values of our own choosing. But this comes at a price: the design of the fundamental physical constants in our universe will be arbitrary to a large extent unless we introduce some other constraints, such as the constraint that our universe should be capable of harboring intelligent life, in which case the choices will have to be narrowed down considerably. But it will still be arbitrary.
On the other hand, we could consider deriving all of our fundamental physical constants from just a single universal fundamental entity (which we might call Ψ, the Greek letter psi, perhaps some sort of master cosmic wave function). To an outside observer it would appear that by so doing we will be tying down our hands even further, that we will have no choice in the creation of our alternate universe. Let us assume that a formula is discovered some time into the future that enables us to derive all of the known important physical constants from just one single fundamental entity that cannot be derived from anything else (indeed this is the main end objective of all “unified field theories” and their epitome the “theory of everything” which would bring theoretical physics to its end conclusion), an entity we are calling Ψ. Then by varying this single fundamental quantity we would be able to change the speed of light to whatever value we want it to have. But if all other physical constants are to be derived directly from this entity, we would automatically alter the values of all the other remaining derivable physical constants. Even if Ψ itself is not a fundamental universal constant but is instead derivable from another yet more fundamental entity, which we may call ω (this is the Greek letter omega), at least in theory we could vary this most fundamental constant of them all in order to vary the derivable quantity Ψ with the end purpose of changing the speed of light to a value we would like to have. But in so doing we will have altered the values of all of the other derivable physical constants. It doesn’t matter how far back we carry the argument all the way into infinity itself, the situation remains the same; we are only shifting the choices somewhere else. So we would appear to have no choice in the creation of our alternate universe. However, we must not forget that since we are deriving from a single universal entity a set of different physical constants, then we are using a different rule for the derivation of each physical constant, and at the very moment when we specify each rule we will be choosing the value each physical constant to whatever we would like for it to be, and the selection of each rule would also be entirely arbitrary, completely up to us. In effect, each rule would be part of the set of initial conditions available to us in our design. We still have the same freedom of choice as we had before, except that instead of specifying different fundamental constants we would be specifying different rules for deriving those constants from a single entity. On the face of it, it appears to be just a matter of choice: we can either specify arbitrarily (or within certain constraints, so as to allow intelligent life to evolve in our creation) a set of n different fundamental physical constants not derivable from anything else, or we can specify arbitrarily a set of n different rules that will allow us to derive that many physical constants from a single more fundamental entity. However, this is just mere speculation, and it may turn out that due to some other requirement or constraint not previously foreseen we could be forced to choose between one of these two alternatives, or between a mixture of these two alternatives.
To the intelligent life forms that may evolve in our universe, if they find a logical framework within which they can numerically derive the values of all known physical constants known to them from a single entity, many of them will take such a fact for granted and will argue that it is the way their Nature works, without seeing any design intention written into their laws of Nature. But this really would not hide completely a basic truth, for even if all of the fundamental physical constants could be derived from a single entity, we would still be leaving the footprints of our design in the very rules that will dictate how all of the known physical constants are to be derived from such a universal entity. We could expect many of the inhabitants inside our creation to argue among them into believing that the rules from which all known physical constants are derived were all the product of sheer random lucky coincidences. But perhaps allowing such beliefs to take place inside our creation would be the ultimate compliment to our unselfishness, for we would be allowing the creatures born to life inside our creation the full free will to believe whatever they so desire. Even a simple thing such as a sequence of fifty or a hundred prime numbers inscribed in the rules that govern the relationship between all of the fundamental physical constants could reveal sooner or later to the inhabitants of our creation some concrete proof of our existence, thus taking away from them the capability of choosing their own set of beliefs. However, there is a limit to the amount of information that can be concealed from them, for as soon as they begin to uncover the rules under which our creation operates and they begin to work backwards in time, as time goes on they will come closer and closer to the realization that many of the things they are witnessing are a near statistical impossibility, extremely hard to account for solely on the basis of an extremely lucky balancing act between randomness and order.